Lecture 19: Least squares fitting

… time to starting thinking about ~~Christmas~~ ~~data~~ coursework! :(

Module feedback: https://leeds.bluera.com/leeds

<Figure size 400x300 with 0 Axes>

Motivation

• Suppose we are given data point representing a quantity over time.

• We want to represent the graph of this data as a simple curve.

• The examples on the following slide show the fitting of two different curves through some experimental data:

  • a straight line;

  • a quadratic curve.

Weekly earnings

/tmp/ipykernel_2358/813076782.py:3: FutureWarning: Passing bytes to 'read_excel' is deprecated and will be removed in a future version. To read from a byte string, wrap it in a `BytesIO` object.
  df = pd.read_excel(r.content, sheet_name="1. AWE Total Pay")
/tmp/ipykernel_2358/813076782.py:6: UserWarning: Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.
  df["date"] = pd.to_datetime(df["date"], errors="coerce")

Raw data for average UK weekly earnings since 2008 (from ONS)

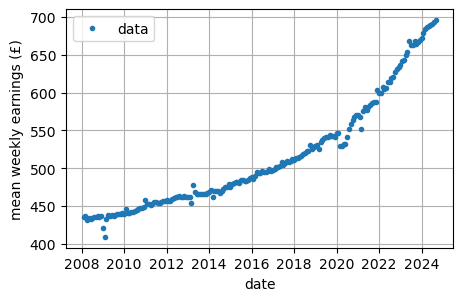
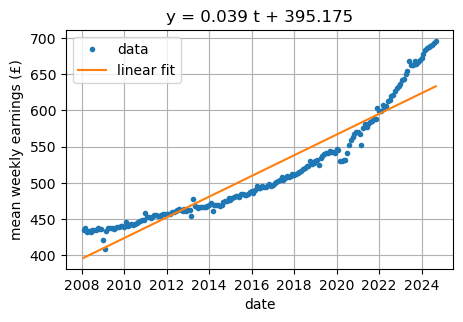
Raw data for weekly earning with a straight line of best fit:

Raw data for weekly earnings with a quadric curve of best fit:

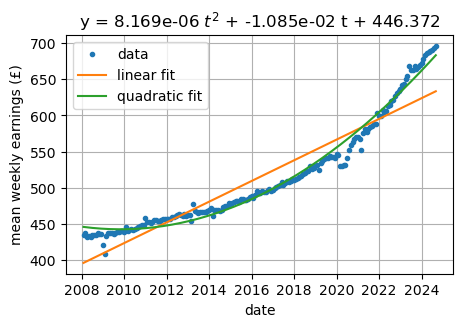
…. how do we do this….

An example of best linear fit

Suppose that the following measured data, \(y\), is observed at different times \(t\):

\[\begin{split} \begin{array}{c|cccc} t & 1 & 2 & 3 & 4 \\ \hline y & 1 & 1.5 & 2.5 & 3.5 \end{array} \end{split}\]

\[\begin{split} \begin{array}{c|cccc} t & 1 & 2 & 3 & 4 \\ \hline y & 1 & 1.5 & 2.5 & 3.5 \end{array} \end{split}\]

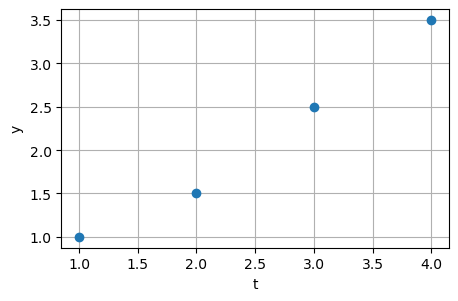
• Suppose we want to represent the data using a straight line: \(y = m t + c\)

• An exact fit would require the following equations to be satisfied:

\[\begin{split} \begin{aligned} m \times 1 + c & = 1 \\ m \times 2 + c & = 1.5 \\ m \times 3 + c & = 2.5 \\ m \times 4 + c & = 3.5. \end{aligned} \end{split}\]

This is a system of linear equations for \((m , c)\) but there are too many equations!

An example of best quadratic fit

Suppose that the following measured data, \(y\), is observed at different times \(t\):

\[\begin{split} \begin{array}{c|ccccc} t & -1.0 & -0.5 & 0 & 0.5 & 1.0 \\ \hline y & 1.0 & 0.5 & 0.0 & 0.5 & 2.0 \end{array} \end{split}\]

\[\begin{split} \begin{array}{c|ccccc} t & -1.0 & -0.5 & 0 & 0.5 & 1.0 \\ \hline y & 1.0 & 0.5 & 0.0 & 0.5 & 2.0 \end{array} \end{split}\]

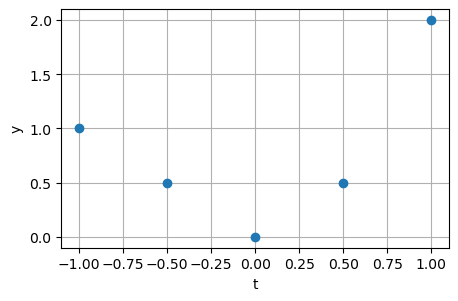
• Consider representing this data as a quadratic line:

  \[ y = a + b t + c t^2 \]

• An exact fit would require the following equations to be satisfied:

  \[\begin{split} \begin{aligned} a + b \times -1 + c \times (-1)^2 & = 1 \\ a + b \times -0.5 + c \times (-0.5)^2 & = 0.5 \\ a + b \times 0 + c \times 0^2 & = 0 \\ a + b \times 0.5 + c \times 0.5^2 & = 0.5 \\ a + b \times 1 + c \times 1^2 & = 2. \end{aligned} \end{split}\]

We recognise this as a system of linear equations for \((a, b, c)\) - but there are too many equations!!

Best approximation

Given that there is no exact fit solution to these overdetermined systems of equations what should we do?

What can we do?

Recall the definition of the residual for the system \(A \vec{x} = \vec{b}\):

\[ \vec{r} = \vec{b} - A \vec{x}, \]

• When \(\vec{r} = \vec{0}\), then \(\vec{x} = \vec{x}^*\) the exact solution.

• When there is no exact solution the next best thing is to make \(\vec{r}\) as small as possible.

• This means finding \(\vec{x}\) that minimises \(\| \vec{r} \|^2\).

The normal equations

It turns out that the \(\vec{x}\) that minimises \(\|\vec{b} - A \vec{x}\|^2\) is the same \(\vec{x}\) that satisfies the following square system of equations:

\[ A^T A \vec{x} = A^T \vec{b} \]

The normal equations

• These equations are referred to as the normal equations for the overdetermined system \(A \vec{x} = \vec{b}\).

• The square matrix \(A^T A\) is generally non-singular (i.e., the solution is unique).

• You can find this solution using Gaussian elimination (for example).

• The normal equations, when solved, give the best solution to the original problem in the sense of minimising the Euclidean norm of the residual.

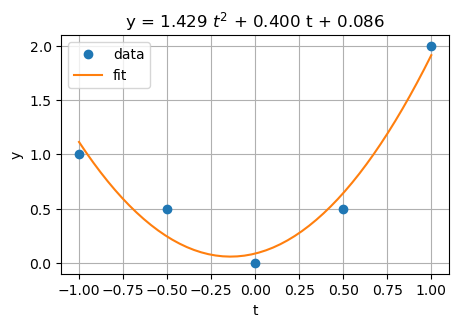
Example 1

Find the least squares approximation to the match the data:

\[\begin{split} \begin{array}{c|ccccc} t & -1.0 & -0.5 & 0 & 0.5 & 1.0 \\ \hline y & 1.0 & 0.5 & 0.0 & 0.5 & 2.0 \end{array} \end{split}\]

Problems with the normal equations

Consider the matrix \(A = \begin{pmatrix} 1 & 1 \\ \varepsilon & 0 \\ 0 & \varepsilon \end{pmatrix}\), which gives

\[\begin{split} A^T A = \begin{pmatrix} 1 + \varepsilon^2 & 1 \\ 1 & 1 + \varepsilon^2. \end{pmatrix} \end{split}\]

If \(\varepsilon \approx \sqrt{eps}\) then the effects of rounding error can make \(A^T A\) appear to be singular.

See also: Nick Higham, Seven sins of numerical linear algebra

Sensitivity and conditioning

• The condition number of a square matrix \(A\) describes how close that matrix is to being singular.

• If the condition number is larger then \(A\) is “close” to being singular.

• When the condition number is very large it is likely that the effects of rounding errors will be most serious: we refer to such a system as being ill-conditioned.

• The normal equations are typically quite ill-conditioned and so it is essential to use high precision arithmetic to solve them and specialised algorithms.

Summary

• Overdetermined systems are common in data modelling and they typically have no solution.

• Even so, it is possible to find a closest solution to the problem.

• It is common to measure this closeness in the Euclidean norm and this leads naturally to the least squares approximation.

• A solution to this problem can be found by solving the normal equations but can must be taken to use arithmetic with sufficient precision and specialised algorithms.