Lecture 18: Robust nonlinear solvers

The problem

Given a continuous function \(f(x)\), the problem is to find a point \(x^*\) such that \(f(x^*) = 0\). That is, \(x^*\) is a solution of the equation \(f(x) = 0\) and is called a root of \(f(x)\).

Summary so far

	Bisection	Newton’s method	Modified Newton	Secant
Simple algorithm	yes	yes	yes	yes
Starting values	bracket	one	one	two
Iterations	lots	normally fewer	similar to Newton	similar to Newton
Function evals	one per iteration	f and df per iteration	two per iteration	one per iteration
Convergence	with good bracket	not always	not always	not always
Turing point roots	no	slower	slower	slower
Use of derivative	no	yes	no	no

The big idea

Combine the robustness of the bisection but improve the estimate using the secant method.

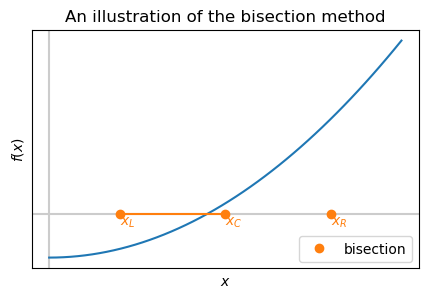
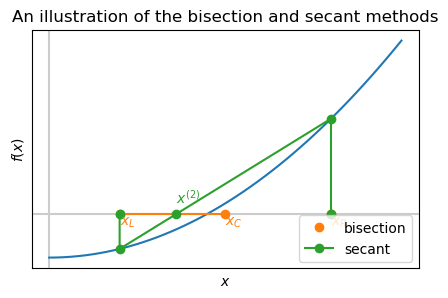
The bisection method doesn’t use the values of \(f\) only it’s sign. Use the values of \(f\) at the end points to improve the convergence rate.

False position method (regula falisi)

The idea is to take the bisection method but instead of evaluating f and the midpoint of \((x_L, x_R)\) and computing signs, we evaluate at the point obtained from the application of the secant method to \(x_L, x_R\):

def false_position(func, a, b, tol=1.0e-10):
    # Starting values
    fa = func(a)
    fb = func(b)
    fc = tol + 1

    while b - a > tol and abs(fc) > tol:
        # Find new point **using secant method**
        c = b - fb * (b - a) / (fb - fa)
        fc = func(c)

        # if root is in left half of interval
        if fa * fc < 0.0:
            # move right end
            b = c
            fb = fc
        else:
            # otherwise,
            # move the left end
            a = c
            fa = fc

    return c

Example

A simply example \(f(x) = x^2 - 2\) starting from bracket \((1, 2)\).

What happens to the right end of the bracket?

def f(x):
    return x * x - 2.0


false_position_with_table(f, 1.0, 2.0, tol=1.0e-4)

it	a	f(a)	b	f(b)	c	f(c)
0	1.000000	-1.000000	2.000000	2.000000	--	--
1	1.333333	-0.222222	2.000000	2.000000	1.333333	-0.222222
2	1.400000	-0.040000	2.000000	2.000000	1.400000	-0.040000
3	1.411765	-0.006920	2.000000	2.000000	1.411765	-0.006920
4	1.413793	-0.001189	2.000000	2.000000	1.413793	-0.001189
5	1.414141	-0.000204	2.000000	2.000000	1.414141	-0.000204
6	1.414201	-0.000035	2.000000	2.000000	1.414201	-0.000035

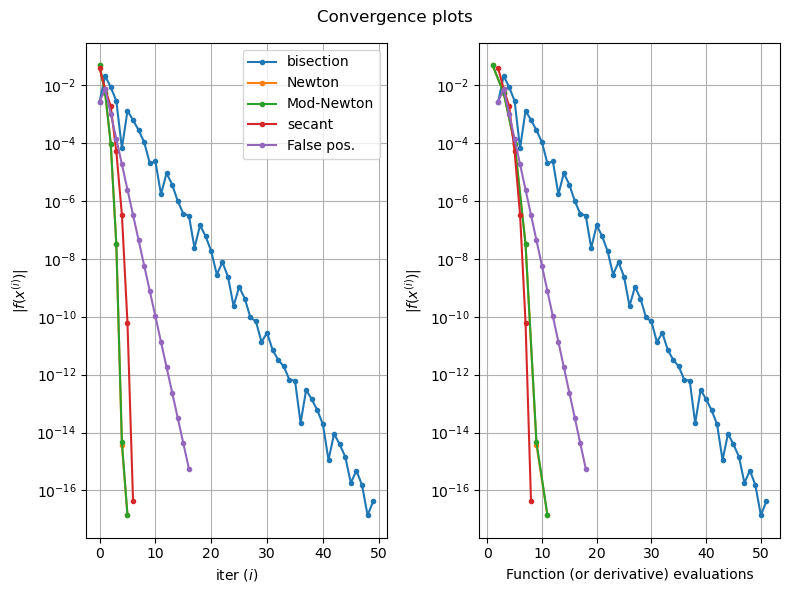
Dekker’s method

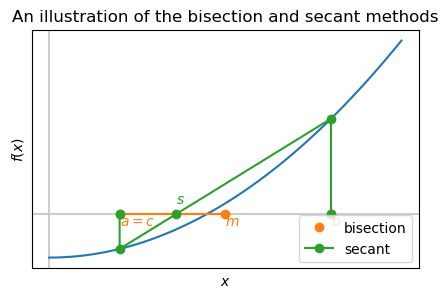
This is a another hybrid method that combines the bisection and secant method.

We find two candidates for approximating the root - given by the secant method and by the bisection method. \(b\) becomes the new estimate of the root and \(a\) is updated to maintain the bracket.

The function requires both an initial bracket:

def dekker(func, a, b, tol=1.0e-10):
    assert func(a) * func(b) < 0  # ensure we have a bracket
    c = a  # start old b at a
    assert abs(b - c) > tol  # ensure we have b != c

def dekker(func, a, b, tol=1.0e-10):
    # start at old b at a
    c = a

    while abs(f(b)) > tol:
        # generate two possible estimates
        m = midpoint_update(func, a, b)
        try:
            s = secant_update(func, b, c)
        except ZeroDivisionError:
            s = m

        # choose best b and update c
        b, c = update_b(b, s, m), b

        # choose a to form a bracket
        a = update_a(func, a, b, c)

        # choose best value for iteration from a and b
        a, b = best_ab(func, a, b)

    return b

def secant_update(func, x, xn):
    return x - func(x) * (x - xn) / (func(x) - func(xn))


def midpoint_update(func, xL, xR):
    return (xL + xR) / 2

def update_b(b, s, m):
    # if s lies strictly between m and b
    if (m < s and s < b) or (b < s and s < m):
        # b <- s (secant)
        return s
    else:
        # b <- m (midpoint)
        return m

def update_a(func, a, b, c):
    # set a to be either a or c so that f(a)*f(b) < 0
    if func(a) * func(b) < 0:
        # (a, b) form a bracket: a <- a
        return a
    elif func(c) * func(b) < 0:
        # (c, b) form a bracket: a <- c
        return c
    else:
        raise Exception("No bracket found")

def best_ab(func, a, b):
    # if a is better estimate
    if abs(func(a)) < abs(func(b)):
        # swap!
        return b, a
    else:
        # don't swap!
        return a, b

Examples

A simply example \(f(x) = x^2 - 2\) starting from bracket \((1, 2)\)

What happens to the left end of the bracket?

def f(x):
    return x * x - 2


dekker(f, a=1.0, b=2.0, tol=1.0e-4)

it	a	f(a)	b	f(b)	update
0	1.000000	-1.000000	2.000000	2.000000	None
1	1.000000	-1.000000	1.500000	0.250000	midpoint
2	1.000000	-1.000000	1.428571	0.040816	secant
3	1.000000	-1.000000	1.414634	0.001190	secant
4	1.000000	-1.000000	1.414216	0.000006	secant

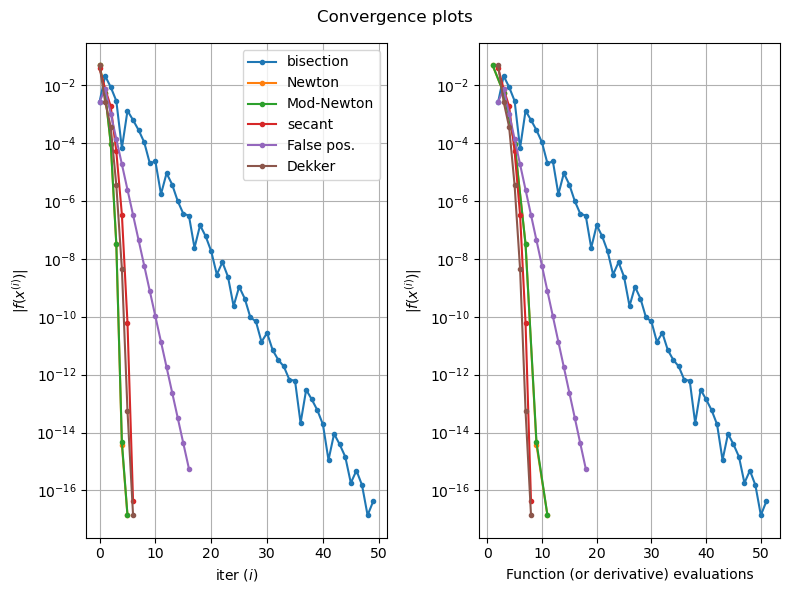
Summary

	Bisection	Newton’s method	Modified Newton	Secant	False position	Dekker
Simple algorithm	yes	yes	yes	yes	yes	more complicated
Starting values	bracket	one	one	two	bracket	bracket
Iterations	lots	normally fewer	similar to Newton	similar to Newton	middle	similar to Newton
Function evals	one per iteration	f and df per iteration	two per iteration	one per iteration	one per iteration	one per iteration
Convergence	with good bracket	not always	not always	not always	with good bracket	with good bracket
Turing point roots	no	slower	slower	slower	no	no
Use of derivative	no	yes	no	no	no	no