This week

This week#

An introduction to nonlinear solvers#

Why do we need nonlinear solvers?#

Given a continuous function \(f(x)\), the problem is to find a point \(x^*\) such that \(f(x^*) = 0\). That is, \(x^*\) is a solution of the equation \(f(x) = 0\) and is called a root of \(f(x)\).

Examples#

  1. The linear equation \(f(x) = a x + b = 0\) has a single solution at \(x^* = -\frac{b}{a}\).

  2. The quadratic equation \(f(x) = a x^2 + b x + c = 0\) is nonlinear , but simple enough to have a known formula for the solutions

    \[ x^* = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. \]

  3. A general nonlinear equation \(f(x) = 0\) rarely has a formula like those above which can be used to calculate its roots.

Example from two years ago’s exam paper#

We want to solve the quadratic equation

\[f(x) = x^2 -(m+\frac{1}{m}) x + 1 = 0\]

for large values of \(m\). The exact solutions are \(m\) and \(\frac{1}{m}\).

# implementation of quadratic formula
def quad(a, b, c):
    """
    Return the roots of the quadratic polynomial a x^2 + b x + c = 0.
    """
    d = np.sqrt(b * b - 4 * a * c)
    return (-b + d) / (2 * a), (-b - d) / (2 * a)

# test for m = 1e8
m = 1e8
roots = quad(1, -(m + 1 / m), 1)

print(f"{roots=}")

roots=(100000000.0, 1.4901161193847656e-08)

# absolute and relative errors
exact_roots = (m, 1 / m)

abs_error = (abs(roots[0] - exact_roots[0]), abs(roots[1] - exact_roots[1]))
rel_error = (abs_error[0] / m, abs_error[1] / (1 / m))

print(f"{abs_error=}")
print(f"{rel_error=}")

abs_error=(0.0, 4.901161193847656e-09)
rel_error=(0.0, 0.49011611938476557)

The need for implicit time stepping methods (1)#

Consider the differential equation

\[ x'(t) = - 2 x(t), \qquad \text{ subject to } \quad x(0) = 1. \]
def rhs1(x, t):
    return -2 * x


def euler(x0, dt, T, rhs):
    # initialise memory
    n = int(T / dt)
    x = np.empty(n + 1)
    t = np.empty(n + 1)

    # starting values
    x[0] = x0
    t[0] = 0.0

    # do the time loop
    for j in range(n):
        x[j + 1] = x[j] + dt * rhs(x[j], t[j])
        t[j + 1] = t[j] + dt

    return x, t
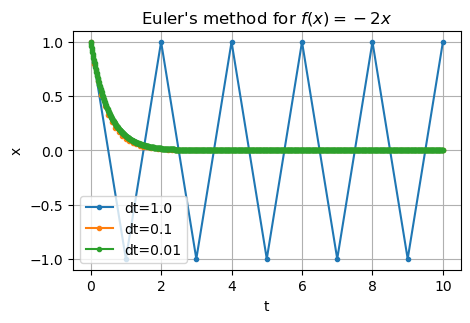
../_images/9966cea5205a08733588bb9c08dd338fe8ae2edc930deb02ef62b18501f9941e.png

Recall explicit Euler says:

\[ x^{(j+1)} = x^{(j)} + \mathrm{dt} f(t^{(j)}, x^{(j)}) \]

Consider instead the implicit Euler method:

\[ x^{(j+1)} = x^{(j)} + \mathrm{dt} f(t^{(j+1)}, x^{(j+1)}) \]

We can’t simply evaluate the right hand side since we don’t know \(x^{(j+1)}\) yet!

For \(f(x, t) = -2x\), we can compute that

\[\begin{split} \begin{aligned} x^{(j+1)} & = x^{(j)} + \mathrm{dt} \, f(t^{(j+1)}, x^{(j+1)}) \\ & = x^{(j)} - 2 \, \mathrm{dt} \, x^{(j+1)} \\ (1 + 2 \Delta t) x^{(j+1)} & = x^{(j)} \\ x^{(j+1)} & = \frac{1}{1 + 2 \mathrm{dt}} x^{(j)}. \end{aligned} \end{split}\]
def implicit_euler(x0, dt, T):
    # initialise memory
    n = int(T / dt)
    x = np.empty(n + 1)
    t = np.empty(n + 1)

    # starting values
    x[0] = x0
    t[0] = 0.0

    # do the time loop
    for j in range(n):
        x[j + 1] = x[j] / (1.0 + 2.0 * dt)
        t[j + 1] = t[j] + dt

    return x, t
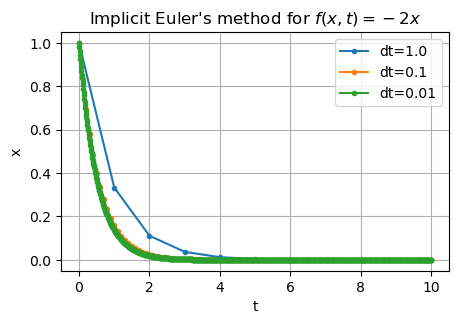
../_images/ffdc330d8d21439ed09f071b3ed301a131cf6c5870b839909ec5ff51302c15e8.png

The need for implicit time stepping methods (2)#

Consider the differential equation

\[ x'(t) = - 2 x(t)^3 \exp(-(1-x(t)^2)), \qquad \text{ subject to } \quad x(0) = 1. \]
def rhs2(x, t):
    return -2 * x**3 * np.exp(-(1 - x**2))
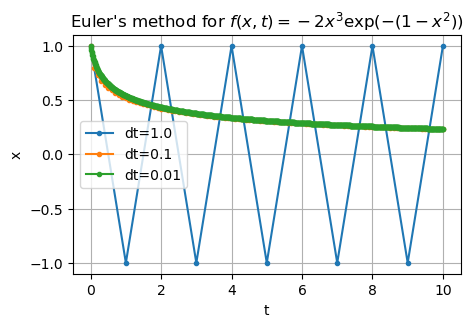
../_images/bb996906b89ea1c9773fa6eb81e88f2e100e9ae9f29510fa4fbfe77dc3a01514.png

We might wish to use an implicit method, but how can we undo \(f\)??

Use a nonlinear solver!

Other difficult problems (1)#

The following formula allows the monthly repayments (\(M\)) on a compound interest mortgage (for a borrowing of \(P\)) to be calculated based upon an annual interest rate of \(r\)% and \(n\) monthly payments (more details).

\[ M = P \frac{\frac{r}{1200} \left(1 + \frac{r}{1200}\right)^n}{\left(1 + \frac{r}{12000}\right)^n - 1}. \]

  • Suppose that we wish to work out how many monthly repayments of £1,000 would be required to repay a mortgage of £150,000 at an annual rate of 5%.

  • This would require us to solve \(f(n) = 0\) where \(f(n) = 1000 - 150000 \frac{\frac{5}{1200}(1+\frac{5}{1200})^n}{(1+\frac{5}{1200})^n - 1}\).

Other difficult problems (2)#

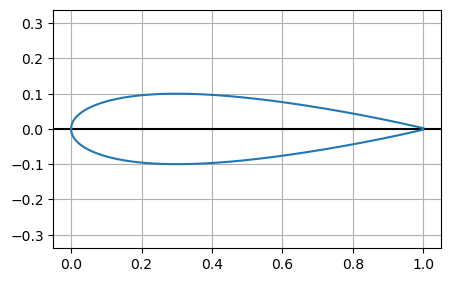
Consider the NACA0012 prototype wing section, which is often used for testing computational methods for simulating flows in aerodynamics

The profile is given by

\[ y^{\pm}(x) = \pm(0.2969 \sqrt{x} - 0.126 x - 0.3516 x^2 + 0.2843 x^3 - 0.1015 x^4), \]

in which \(+\) gives the upper surface and \(-\) gives the lower surface.

Find the point \(x\) at which the thickness \(t\) of the aerofoil is \(0.1\), i.e. solve \(f(x) = 0\) where \(f(x) = y^+(x) - y^-(x) - 0.1\).

  • There will be two solutions for \(x\) for this value of \(t\).

../_images/020beb6310162802994165513acd0dba8096adb432d9d7d8b747d0226d503e01.png

The bisection method#

  1. Suppose the know there is a root \(x^*\) (\(f(x^*) = 0\)) between two end points \(a\) and \(b\)

  2. Call \(c = \dfrac{a+b}{2}\), then the solution is either between \(a\) and \(c\) or between \(c\) and \(b\)

  3. If the solution is between \(a\) and \(c\)

    • then go to step 1. with the end points as \(a\) and \(c\)

    • otherwise, go to step 1. with the end points as \(c\) and \(b\)

How can we tell that we have a solution between \(a\) and \(b\)?

How do we know we have a solution between \(a\) and \(b\)?#

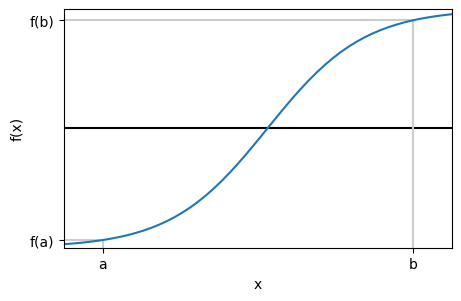
../_images/8504a1970436aa000308136e41ca6152fc06d0b8f9dcf363e44f2221afb7fcec.png

We test if \(f(a)\) and \(f(b)\) have opposite signs!

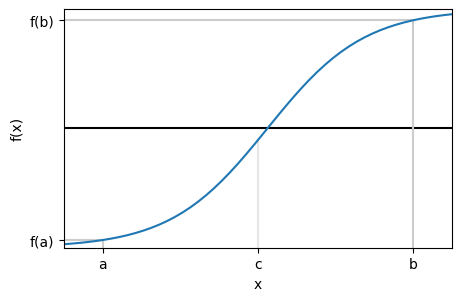
../_images/0bda71fc231af227b6508e137c7a91bc027941aee435b662ad6b81af2c58c1ce.png

\(f(a)\) and \(f(c)\) have opposite signs so solution is between \(c\) and \(b\)!

# Simple bisection implementation
def bisection(func, a, b, tol=1.0e-10):
    # Starting values
    fa = func(a)
    fb = func(b)

    while b - a > tol:
        # Find new mid point
        c = (a + b) / 2
        fc = func(c)

        # if root is in left half of interval
        if fa * fc < 0.0:
            # move right end
            b = c
            fb = fc
        else:
            # otherwise,
            # move the left end
            a = c
            fa = fc

    return (a + b) / 2

Implict Euler with bisection for the nonlinear solve#

Recall the differential equation:

\[ x'(t) = - 2 x(t)^3 \exp(-(1-x(t)^2)), \qquad \text{ subject to } \quad x(0) = 1. \]

Recall the implicit Euler method:

\[ x^{(j+1)} = x^{(j)} + \mathrm{dt} f(t^{(j+1)}, x^{(j+1)}) \]

We cast this as a nonlinear equation to solve at each timestep: Find \(x^{(j+1)}\) such that

\[ F(x^{(j+1)}) := x^{(j+1)} - x^{(j)} - \mathrm{dt} f(t^{(j+1)}, x^{(j+1)}) = 0. \]
def implicit_euler(x0, dt, T):
    # initialise memory
    n = int(T / dt)
    x = np.empty(n + 1)
    t = np.empty(n + 1)

    # starting values
    x[0] = x0
    t[0] = 0.0

    # time loop
    for j in range(n):
        t[j + 1] = t[j] + dt

        # nonlinear function to solve each time step
        def F(xnew):
            return xnew - x[j] - dt * rhs2(xnew, t[j + 1])

        # perform the nonlinear solve
        x[j + 1] = bisection(F, -1.0, 1.0)

    return x, t
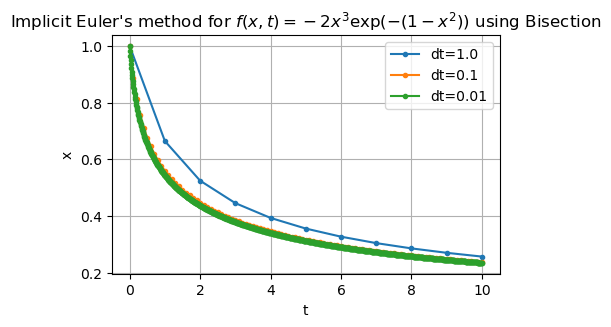
../_images/110c3ebb8c7ee516a7747c18ec5acc254f08e5980ddaee1a637d8d105a26a4cd.png

Example 2#

Use the bisection method to calculate the number of monthly repayments of £1,000 that are required to repay a mortgage of £150,000 at an annual rate of 5%.

It is clear that 1 monthly repayment (\(n=1\)) will not be sufficient, whilst we should try a very large value of \(n\) to try to bracket the correct solution.

M = 1000
P = 150000
r = 5


def f(x):
    return M - P * ((r / 1200) * (1 + r / 1200) ** x) / ((1 + r / 1200) ** x - 1)
it a b c f(a) $\times$ f(c) sign(f(a) $\times$ f(c)) update
0 1.00 1000.00 500.50 -4.28e+07 negative b <- c
1 1.00 500.50 250.75 -5.19e+06 negative b <- c
2 1.00 250.75 125.88 7.99e+07 positive a <- c
3 125.88 250.75 188.31 8.06e+04 positive a <- c
4 188.31 250.75 219.53 6.66e+03 positive a <- c
5 219.53 250.75 235.14 8.26e+01 positive a <- c
6 235.14 250.75 242.95 -3.20e+01 negative b <- c
7 235.14 242.95 239.04 -1.45e+01 negative b <- c
8 235.14 239.04 237.09 -5.59e+00 negative b <- c
9 235.14 237.09 236.12 -1.06e+00 negative b <- c
10 235.14 236.12 235.63 1.22e+00 positive a <- c
11 235.63 236.12 235.87 2.73e-02 positive a <- c
12 235.87 236.12 235.99 -1.10e-02 negative b <- c
13 235.87 235.99 235.93 -4.62e-03 negative b <- c

Example 3#

Use the bisection method to find the points at which the thickness of the NACA0012 aerofoil is 0.1 with an error of less than \(10^{-4}\).

It can be seen that \(0 \le x^* \le 1\) but there are two solutions in this interval, so try \([x_L, x_R] = [0.5, 1]\) as the initial bracket.

def f(x):
    yp = (
        -0.1015 * np.power(x, 4)
        + 0.2843 * np.power(x, 3)
        - 0.3516 * np.power(x, 2)
        - 0.126 * x
        + 0.2969 * np.sqrt(x)
    )
    t = 0.1
    return yp - 0.5 * t
it a b c f(a) $\times$ f(c) sign(f(a) $\times$ f(c)) update
0 0.50000 1.00000 0.75000 1.02152e-04 positive a <- c
1 0.75000 1.00000 0.87500 -5.54603e-05 negative b <- c
2 0.75000 0.87500 0.81250 -2.29940e-05 negative b <- c
3 0.75000 0.81250 0.78125 -7.63859e-06 negative b <- c
4 0.75000 0.78125 0.76562 -1.77701e-07 negative b <- c
5 0.75000 0.76562 0.75781 3.49847e-06 positive a <- c
6 0.75781 0.76562 0.76172 8.15966e-07 positive a <- c
7 0.76172 0.76562 0.76367 1.73699e-07 positive a <- c
8 0.76367 0.76562 0.76465 2.96088e-08 positive a <- c
9 0.76465 0.76562 0.76514 2.11193e-09 positive a <- c
10 0.76514 0.76562 0.76538 -4.63408e-10 negative b <- c
11 0.76514 0.76538 0.76526 -3.40195e-11 negative b <- c
12 0.76514 0.76526 0.76520 1.80650e-10 positive a <- c

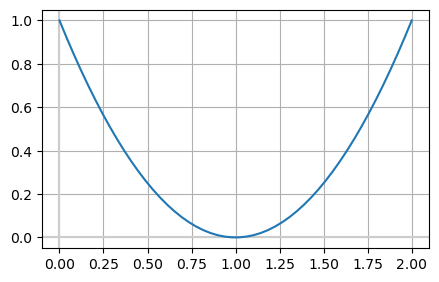
Example 4#

What about if the root is a turning point?

\[ f(x) = (x-1)^2 = x^2 - 2x + 1. \]
../_images/0fd3ff97733ce009e341fdf122aa7c94183c27092d2ea9fc97ecda65faca1c2b.png

Summary#

Bisection

Simple algorithm

yes

Starting values

bracket

Iterations

lots

Function evals

one per iteration

Convergence

with good bracket

Turing point roots

no

Use of derivative

no

Coursework clarifications#

Portfolio

  • Best 6 out of 8 sections count for your final grade

  • If you have full marks on the first 6 sections, the final two sections don’t count!

Final coursework

  • Deadline is Wed 18 Dec

  • Your submission should be an evaluated jupyter notebook (.ipynb)

Recap of the bisection method#

  1. Suppose the know there is a root \(x^*\) (\(f(x^*) = 0\)) between two end points \(a\) and \(b\)

  2. Call \(c = \dfrac{a+b}{2}\), then the solution is either between \(a\) and \(c\) or between \(c\) and \(b\)

  3. If the solution is between \(a\) and \(c\)

    • then go to step 1. with the end points as \(a\) and \(c\)

    • otherwise, go to step 1. with the end points as \(c\) and \(b\)

Bisection challenges (i)#

  • How to determine an initial bracket \((a, b)\)?

    • You need to have that \(f(a) \times f(b) < 0\) - i.e. there is a change of sign!

    • If \(f(x) \ge 0\) for all \(x\), bisection is not possible

    • If \(f(a) = 0\) or \(f(b) = 0\), then you have already found the route and you can stop!

    • Big brackets take a long time to get small

Bisection challenges (ii)#

  • How do you know you’ve still trapped the root?

    • If \(f(a) \times f(b) < 0\), then either \(f(a) \times f(c) < 0\), \(f(b) \times f(c) < 0\) or \(f(c) = 0\).

sign(\(f(a)\))

sign(\(f(b)\))

sign(\(f(c)\))

root between

positive

negative

positive

\(c\) and \(b\)

positive

negative

negative

\(a\) and \(c\)

negative

positive

positive

\(a\) and \(c\)

negative

positive

negative

\(c\) and \(b\)

any

any

0

root is at \(c\)

Newton’s method#

  • The bisection method needs lots of iterations because it doesn’t take into account the value of the function at the end points of the interval, only the sign

  • We consider now an alternative approach where we use the derivative of the function \(f\) to help improve the convergence rate!

Derivation of Newton’s method#

1. Evaluate function at current guess:#

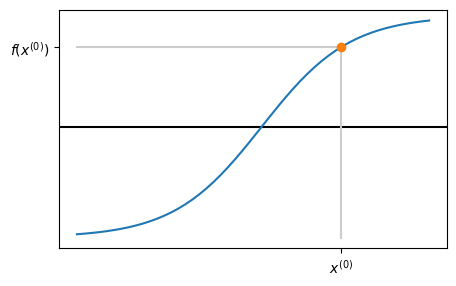
../_images/264714a494871057056672abb7cde6dbc1db5d30109702a5cff33e75a076faac.png

2. Trace tangent line using derivative#

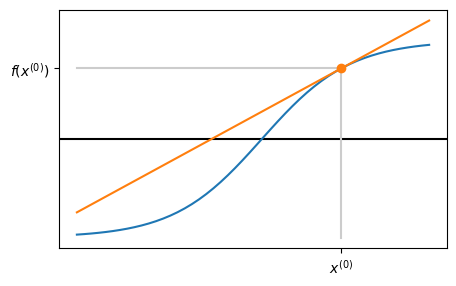
../_images/04da8aba512bce861f0427a369b5e25bbcbf2645ae4a3fd011cd29d2e1ad5830.png

3. Next iterate \(x_1\) is where tangent line crosses \(x\)-axis#

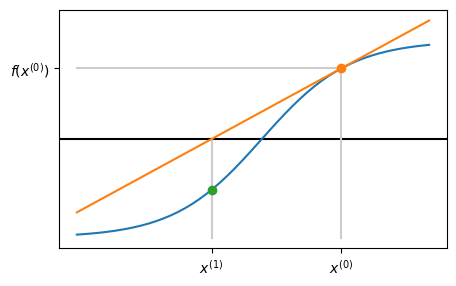
../_images/1856ed0440a92ce33d4de30e7c5d7f1308a8c7126bdfc41ad8b74094cd90b164.png

4. Go back to step 1. and repeat!#

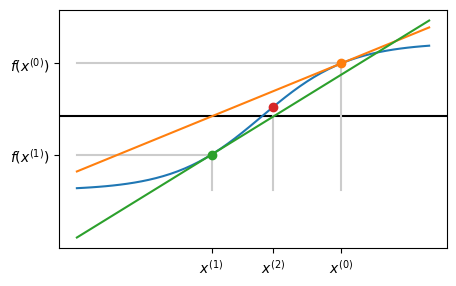
../_images/4fe277058cf0ceec7660d66157137a2116bbdd15c5516b496d162c9f23ba860a.png

So what’s the formula?#

Slope is

\[ f'(x^{(0)}) = \frac{f(x^{(0)}) - 0}{x^{(0)} - x^{(1)}} \]

which rearranges to give

\[ x^{(1)} = x^{(0)} - \frac{f(x^{(0)}}{f'(x^{(0)})}. \]

Python version#

def newton(f, df, x0, tol=1.0e-10):
    x = x0

    while abs(f(x)) > tol:
        x = x - f(x) / df(x)

    return x

def newton2(f, df, x0, tol=1.0e-10):
    x = x0
    fx = f(x)

    while abs(fx) > tol:
        x = x - fx / df(x)
        fx = f(x)  # only one function evaluation per loop

    return x

Examples of Newton’s method#

Starting from \(x^{(0)} = 1\) with \(TOL = 10^{-4}\), we get the root as \(x^* \approx 0.765789\) after 2 iterations for the NACA0012 aerofoil example:

Recall NACA0012 aerofoil example

def f(x):
    t = 0.1

    yp = (
        -0.1015 * np.power(x, 4)
        + 0.2843 * np.power(x, 3)
        - 0.3516 * np.power(x, 2)
        - 0.126 * x
        + 0.2969 * np.sqrt(x)
    )
    f = yp - 0.5 * t

    return f


def df(x):
    dy = (
        -4 * 0.1015 * np.power(x, 3)
        + 3 * 0.2843 * np.power(x, 2)
        - 2 * 0.3516 * x
        - 0.126
        + 0.2969 * 0.5 * np.power(x, -0.5)
    )
    f = dy

    return f

Starting from \(x^{(0)} = 1\) with \(TOL = 10^{-4}\), we get the root as \(x^* \approx 0.765789\) after 2 iterations for the NACA0012 aerofoil example:

iter x f(x)
0 1.000000 -0.047900
1 0.795168 -0.005392
2 0.765789 -0.000096

Starting from \(x^{(0)} = 0.1\) with \(TOL = 10^{-4}\), we get the root as \(x^* \approx 0.033863\) after 5 iterations for the second solution to the NACA0012 aerofoil example.

iter x f(x)
0 0.100000 0.028046
1 0.000278 -0.045086
2 0.005413 -0.028849
3 0.020693 -0.010046
4 0.031958 -0.001300
5 0.033863 -0.000024

Compare against a similar test with the bisection method - the Newton method is much faster!

it a b c f(a) $\times$ f(c) sign(f(a) $\times$ f(c)) update
0 0.50000 1.00000 0.75000 1.02152e-04 positive a <- c
1 0.75000 1.00000 0.87500 -5.54603e-05 negative b <- c
2 0.75000 0.87500 0.81250 -2.29940e-05 negative b <- c
3 0.75000 0.81250 0.78125 -7.63859e-06 negative b <- c
4 0.75000 0.78125 0.76562 -1.77701e-07 negative b <- c
5 0.75000 0.76562 0.75781 3.49847e-06 positive a <- c
6 0.75781 0.76562 0.76172 8.15966e-07 positive a <- c
7 0.76172 0.76562 0.76367 1.73699e-07 positive a <- c
8 0.76367 0.76562 0.76465 2.96088e-08 positive a <- c
9 0.76465 0.76562 0.76514 2.11193e-09 positive a <- c
10 0.76514 0.76562 0.76538 -4.63408e-10 negative b <- c
11 0.76514 0.76538 0.76526 -3.40195e-11 negative b <- c
12 0.76514 0.76526 0.76520 1.80650e-10 positive a <- c

Zero derivative as a root#

  • We saw that the bisection method cannot deal with the situation where a root occurs at a turning point. That is,

    \[ f(x^*) = f'(x^*) = 0. \]

  • At first sight, it may appear that Newton’s method will struggle with such situations since \(x^{(i+1)} = x^{(i)} - \frac{f(x^{(i)})}{f'(x^{(i)})}\) would lead to \(\frac{0}{0}\) occurring when \(x^{(i)} = x^*\).

  • Fortunately, this is not a problem in practice and the iteration can still converge - although it converges more slowly than to a “simple root”.

Zero derivative as a root - example#

Find a solution of \(f(x) = 0\) using Newton’s method when

\[ f(x) = (x-1)^2 = x^2 - 2x + 1. \]

This has a solution \(x^* = 1\), however \(f'(x) = 2x - 2\), so \(f'(x^*) = 0\) when \(x = x^*= 1\).

def f(x):
    return (x - 1) ** 2


def df(x):
    return 2 * (x - 1)

newton_with_table(f, df, x0=4.0, tol=1.0e-4)
iter x f(x)
0 4.000000 9.000000
1 2.500000 2.250000
2 1.750000 0.562500
3 1.375000 0.140625
4 1.187500 0.035156
5 1.093750 0.008789
6 1.046875 0.002197
7 1.023438 0.000549
8 1.011719 0.000137
9 1.005859 0.000034

Problems with Newton’s methods#

When Newton’s method works it is a fast way of solving a nonlinear equation \(f(x) = 0\), but it does not always work.

  1. Consider applying a Newton iteration to the function \(f(x) = x^3 + 2 x^2 + x + 1\) with \(x^{(0)} = 0\).

    This gives \(f'(x) = 3 x^2 + 4 x + 1\). With \(x^{(0)} = 0\) this gives:

def f(x):
    return x**3 + 2 * x**2 + x + 1


def df(x):
    return 3 * x**2 + 4 * x + 1

/tmp/ipykernel_2201/2403100073.py:11: RuntimeWarning: divide by zero encountered in scalar divide
  x = x - f(x) / df(x)
/tmp/ipykernel_2201/475226614.py:2: RuntimeWarning: invalid value encountered in scalar add
  return x**3 + 2 * x**2 + x + 1
iter x f(x)
0 0.000000 1.000000
1 -1.000000 1.000000
2 -inf nan

  1. We can also get cases where the iteration does not “blow up” but diverges slowly…

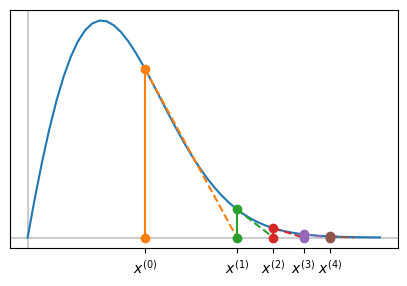
../_images/bf0e06349b7a43fc36d77d600b3cf4bb8a606e3adf24e2e6ed76fdc6186c8104.png

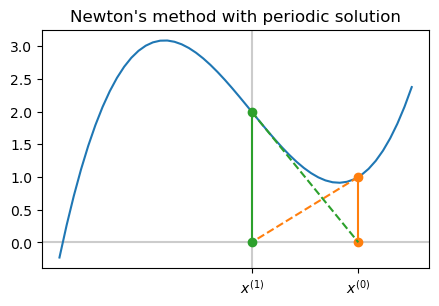
  1. It is even possible for the iteration to simply cycle between two values repeatedly…

def f(t):
    return t**3 - 2 * t + 2


def df(t):
    return 3 * t**2 - 2

WARNING! Newton iteration has not converged. Too many iterations.
iter x f(x)
0 1.000000 1.000000
1 0.000000 2.000000
2 1.000000 1.000000
3 0.000000 2.000000
4 1.000000 1.000000
5 0.000000 2.000000
6 1.000000 1.000000
7 0.000000 2.000000
8 1.000000 1.000000
9 0.000000 2.000000
10 1.000000 1.000000
11 0.000000 2.000000
12 1.000000 1.000000
13 0.000000 2.000000
14 1.000000 1.000000
15 0.000000 2.000000
16 1.000000 1.000000
17 0.000000 2.000000
18 1.000000 1.000000
19 0.000000 2.000000
20 1.000000 1.000000
21 0.000000 2.000000
22 1.000000 1.000000
23 0.000000 2.000000
24 1.000000 1.000000
25 0.000000 2.000000
26 1.000000 1.000000
27 0.000000 2.000000
28 1.000000 1.000000
29 0.000000 2.000000
30 1.000000 1.000000
31 0.000000 2.000000
32 1.000000 1.000000
33 0.000000 2.000000
34 1.000000 1.000000
35 0.000000 2.000000
36 1.000000 1.000000
37 0.000000 2.000000
38 1.000000 1.000000
39 0.000000 2.000000
40 1.000000 1.000000
41 0.000000 2.000000
42 1.000000 1.000000
43 0.000000 2.000000
44 1.000000 1.000000
45 0.000000 2.000000
46 1.000000 1.000000
47 0.000000 2.000000
48 1.000000 1.000000
49 0.000000 2.000000
50 1.000000 1.000000
51 0.000000 2.000000
52 1.000000 1.000000
53 0.000000 2.000000
54 1.000000 1.000000
55 0.000000 2.000000
56 1.000000 1.000000
57 0.000000 2.000000
58 1.000000 1.000000
59 0.000000 2.000000
60 1.000000 1.000000
61 0.000000 2.000000
62 1.000000 1.000000
63 0.000000 2.000000
64 1.000000 1.000000
65 0.000000 2.000000
66 1.000000 1.000000
67 0.000000 2.000000
68 1.000000 1.000000
69 0.000000 2.000000
70 1.000000 1.000000
71 0.000000 2.000000
72 1.000000 1.000000
73 0.000000 2.000000
74 1.000000 1.000000
75 0.000000 2.000000
76 1.000000 1.000000
77 0.000000 2.000000
78 1.000000 1.000000
79 0.000000 2.000000
80 1.000000 1.000000
81 0.000000 2.000000
82 1.000000 1.000000
83 0.000000 2.000000
84 1.000000 1.000000
85 0.000000 2.000000
86 1.000000 1.000000
87 0.000000 2.000000
88 1.000000 1.000000
89 0.000000 2.000000
90 1.000000 1.000000
91 0.000000 2.000000
92 1.000000 1.000000
93 0.000000 2.000000
94 1.000000 1.000000
95 0.000000 2.000000
96 1.000000 1.000000
97 0.000000 2.000000
98 1.000000 1.000000
99 0.000000 2.000000
100 1.000000 1.000000
101 0.000000 2.000000
../_images/d3d0df162fe4c1c1001ed51db0c1a92f7ce133fe2f734d4aa8778e65c36b7315.png

Summary#

Bisection

Newton’s method

Simple algorithm

yes

yes

Starting values

bracket

one

Iterations

lots

normally fewer

Function evals

one per iteration

f and df per iteration

Convergence

with good bracket

not always

Turing point roots

no

slower

Use of derivative

no

yes
Contents