Today: Exact solutions and error#
Tom Ranner
Recap#
Differential equation#
\(f\) is called the right-hand side.
Euler’s method#
Set initial values for \(t^{(0)}\) and \(y^{(0)}\)
Loop over all time steps, until the final time, updaing using the formulae:
\[\begin{split} \begin{aligned} y^{(i+1)} & = y^{(i)} + \mathrm{d}t f(t^{(i)}, y^{(i)}) \\ t^{(i+1)} & = t^{(i)} + \mathrm{d}t. \end{aligned} \end{split}\]
Exact derivatives and exact solutions#
In some cases, it is possible to evaluate derivatives of a function exactly.
In some cases, we can solve a differential equation exactly.
This is not what this module is about, but some special cases will help us to test our methods!
Example 1#
Consider the function \(y(t) = t^2\).
We can plot the function and it’s derivative
We can compute \(y'(t)\) using the definition of a limit
Example 2#
Consider the function \(y(t) = t^3\).
Similarly it is quite easy to compute the derivative!
In general, it can be shown that when \(y(t) = a t^m\), then \(y'(t) = a m t^{m-1}\).
Example 3#
By working backwards from a known expression for \(y(t)\) and \(y'(t)\), we can make up our own differential equation that has \(y(t)\) as a known solution.
Consider, for example, \(y(t) = t^3\), which has \(y'(t) = 3 t^2\).
We see that \(y(t) = t^3\), is the solution of $\( y'(t) = \frac{3 y(t)}{t} \quad\text{subject to the initial condition}\quad y(1) = 1. \)$
So, if we solve this differential equation for \(t\) between \(1\) and \(2\), then we know the exact answer when \(t = 2\) is \(y(2) = 2^3 = 8\).
Errors in Euler’s method#
Solve this differential equation using Euler’s method and check the error at \(t = 2\)
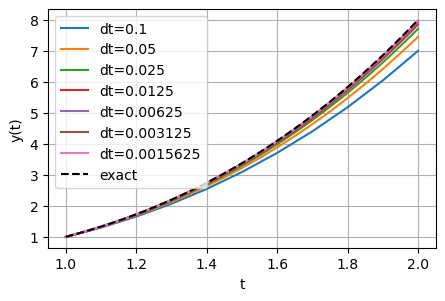
The errors at \(t=2\)#
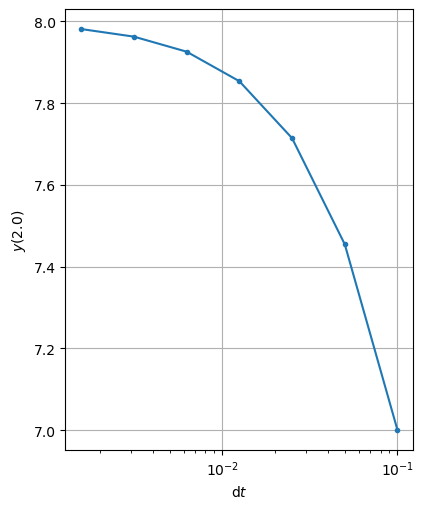
The errors at \(t=2\)#
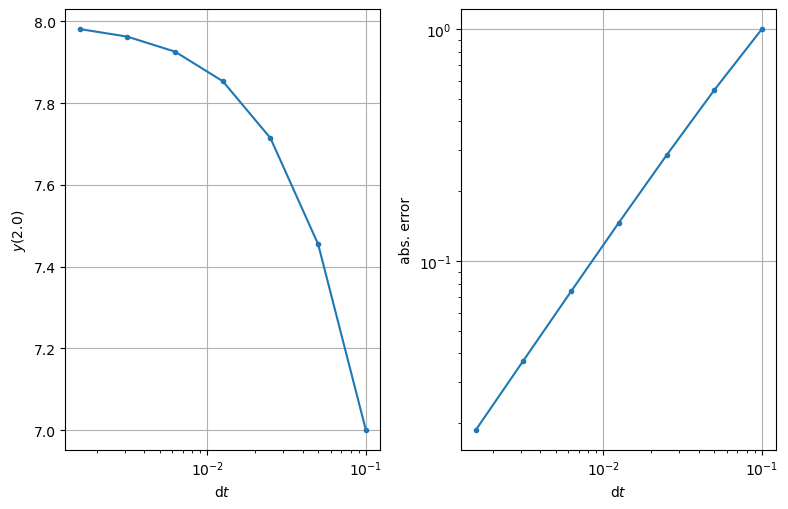
| n | dt | solution | abs. error | ratio |
|---|---|---|---|---|
| 10 | 0.100000 | 7.000000 | 1.000000 | --- |
| 20 | 0.050000 | 7.454545 | 0.545455 | 0.545455 |
| 40 | 0.025000 | 7.714286 | 0.285714 | 0.523810 |
| 80 | 0.012500 | 7.853659 | 0.146341 | 0.512195 |
| 160 | 0.006250 | 7.925926 | 0.074074 | 0.506173 |
| 320 | 0.003125 | 7.962733 | 0.037267 | 0.503106 |
| 640 | 0.001563 | 7.981308 | 0.018692 | 0.501558 |
Each time \(\mathrm{d}t\) is halved the error is halved!?!?!?!?!?!?!?
What might we expect the computed solution to be if we halved \(\mathrm{d}t\) one more time?
Big O Notation#
In considering algorithm complexity, you have already seen big O notation. For example:
Gaussian elimination requires \(O(n^3)\) operations when \(n\) is large.
Backward substitution requires \(O(n^2)\) operations when \(n\) is large.
For large values of \(n\), the highest powers of \(n\) are most significant.
For small values of \(\mathrm{d}t\), it is the lowest power of \(\mathrm{d}t\) that are most significant:
e.g., when \(\mathrm{d}t = 0.001\), \(\mathrm{d}t\) is much bigger than \((\mathrm{d}t)^2\)
We can make use of the “big O” notation in either case.
For example, suppose $\( f(x) = 2 x^2 + 4 x^3 + x^5 + 2 x^6, \)$
then \(f(x) = O(x^6)\) as \(x \to \infty\)
and \(f(x) = O(x^2)\) as \(x \to 0\).
In this notation, we can say that the error in Euler’s method is \(O(\mathrm{d}t)\).
Improving on Euler’s method#
So the error is proportional to \(\mathrm{d}t\), …. so what?
The proposal#
Take one time step of size \(\mathrm{d}t\) - call this solution \(\alpha\)
Take two time steps of size \(\frac{1}{2} \mathrm{d}t\) - call this solution \(\beta\)
The error using \(\beta\) should be about half the error using \(\alpha\):
Rearranging gives: $\( y_{\text{exact}} = 2 \beta - \alpha \)$ which should be an improve approximation!
We use this approach to construct the midpoint method
The midpoint method#
Assume we have already computed up to time step \(i\): \(t^{(i)}\) and \(y^{(i)}\)
Take one time step of size \(\mathrm{d}t\) - call this solution \(\alpha\):
\[\begin{split} \begin{aligned} \alpha & = y^{(i)} + \mathrm{d}t f(t^{(i)}, y^{(i)}) \\ t^{(i+1)} & = t^{(i)} + \mathrm{d} t \end{aligned} \end{split}\]Take two time steps of size \(\frac{1}{2} \mathrm{d}t\) - call this solution \(\beta\):
\[\begin{split} \begin{aligned} k & = y^{(i)} + (\mathrm{d}t / 2) f(t^{(i)}, y^{(i)}) \\ m & = t^{(i)} + \mathrm{d}t / 2 \\ \beta & = k + (\mathrm{d}t / 2) f(m, k) \\ t^{(i+1)} & = m + \mathrm{d}t / 2. \end{aligned} \end{split}\]
Combine \(\alpha\) and \(\beta\) as suggested on the previous slide…
… results in
for i in range(n):
y_mid = y[i] + 0.5 * dt * f(t[i], y[i])
t_mid = t[i] + 0.5 * dt
y[i + 1] = y[i] + dt * f(t_mid, y_mid)
t[i + 1] = t[i] + dt
The results#
We look at the results for the same problem as before for the solution at the final time \(t = 2.0\):
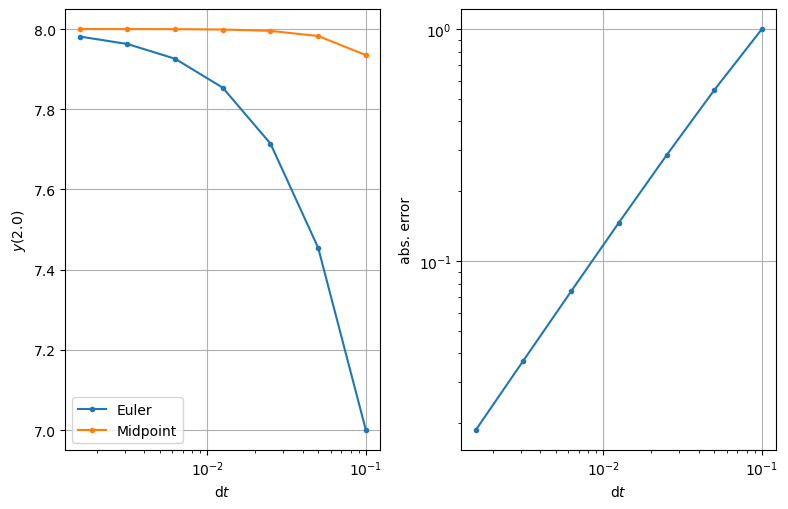
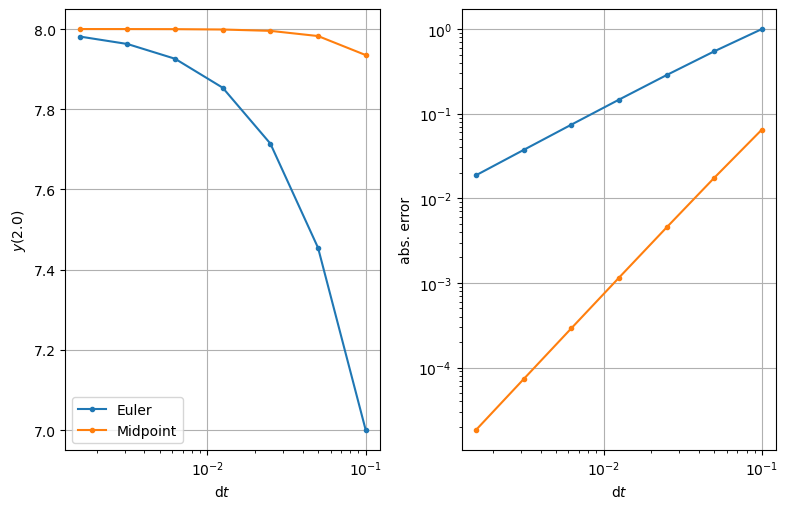
| n | dt | solution | abs. error | ratio |
|---|---|---|---|---|
| 10 | 0.100000 | 7.935060 | 0.064940 | --- |
| 20 | 0.050000 | 7.982538 | 0.017462 | 0.268892 |
| 40 | 0.025000 | 7.995475 | 0.004525 | 0.259127 |
| 80 | 0.012500 | 7.998849 | 0.001151 | 0.254473 |
| 160 | 0.006250 | 7.999710 | 0.000290 | 0.252212 |
| 320 | 0.003125 | 7.999927 | 0.000073 | 0.251100 |
| 640 | 0.001563 | 7.999982 | 0.000018 | 0.250548 |
Each time \(\mathrm{d}t\) is halved the error is quartered!?!?!?!?!?!?!?
What about the big O?#
The error quarters each time that the time interval size \(\mathrm{d}t\) is halved - the error is proportional to \((\mathrm{d}t)^2\).
The error of the midpoint method is \(O(\mathrm{d}t^2)\) as \(\mathrm{d}t \to 0\)
This is a significant improvement over Euler’s method:
Euler is a first order method
the midpoint method is a second order method
Example#
Take two steps of the midpoint method to approximate the solution of
for \(0 \le t \le 1\).
Summary#
In some special cases exact solutions of differential equations can be found - this is not true in general however.
Computational modelling is required for most problems of practical interest (and will of course work just as well even if an exact solution could be found).
Comparison with a known solution shows that Euler’s method leads to an error that is proportional to \(\mathrm{d}t\).
The midpoint scheme’s error is proportional to \((\mathrm{d}t)^2\) but requires about twice the computational work per step.
Only 2 computational schemes are introduced here - there are many more that we don’t consider…

